This village has a secret that almost everybody knows.
And suddenly, the sound of a horn. The horn hadn't been in years. Maybe ever, but everyone intuitively knew its purpose. They were to stop whatever they were doing and march to the village center to listen. To what, they didn't know, but something of undeniable importance for sure. So axes were laid on logs, fishing rods were cast aside, and piles of dough remained unkneaded.
In the village square, a new, weird platform was erected. It stood bare, deprived of a podium or chairs, with the head of the village standing atop it harsh and salient. He waited a long time for the crowd to quiet and began to speak.
“It has always been our way back when the village huts were made of mud. We all know it and adhere to it. To survive here, we have but two rules. The first is we share! The bad and the good, we share the load and the fruit so that we will survive! So that we all thrive! The second is much more important: we say only what needs to be said to a person. We will never insult or congratulate someone to his face.” From the crowd, there was a scream, “But we’ll tell his friends all about it!” All laugh in agreement, The shadow of a smile lingered on the village head's face for a second, “That is more true than not, I'm sorry to say. So we all know about the treasures! We have discussed them in length in hisses and hushes. Aye, the village has many treasures buried under our huts, but our way prevents us from sharing them. I hereby sentence all of us to solitary confinement in our huts until we all decide that we know where the treasure lies. When we are sure each person certain of a treasure can leave his hut and, at the stroke of midnight, start digging. We are only worthy if all treasures are found, and no empty hole is dug. So go home, ponder, and when you feel it's your time to dig, dig.”
And with that, the villagers return to their homes, each armed with their private information, the knowledge of every other villager's treasure status but their own. As the sun sets, the village is silent in anticipation. This silence, however, is not mere tranquility; it's the manifestation of Mutual Information, a concept rooted in the fundamentals of information theory.
Mutual information measures the information that one random variable (in this case, one villager shares with another villager). It quantifies how much knowing one of these variables reduces uncertainty about the other. Over the next three days, we'll see how this concept plays out in the village and how it allows the villagers to find their buried treasures.
So can you guess? On the stroke of midnight on the third day, the sounds of shovels hit the ground, and a sigh of relief was heard. One group that knew about three treasures went to bed, knowing that there was none buried under its hut. The other group was out digging as the night before convinced them that they, indeed, had a treasure. So how did they all know without speaking or gaining new knowledge?
The answer is elegant and simple. During the speech, there were two types of information in the crowd immediately. Most people were told and thus knew about three treasures, but only three individuals knew about two. The entire village slept the first night soundly because they all knew there was at least one treasure, but on the second night, the three stayed awake. Listening. If they knew about all treasures, they should hear the digging start. But it was quiet, and now their knowledge was complete. They indeed had a treasure.
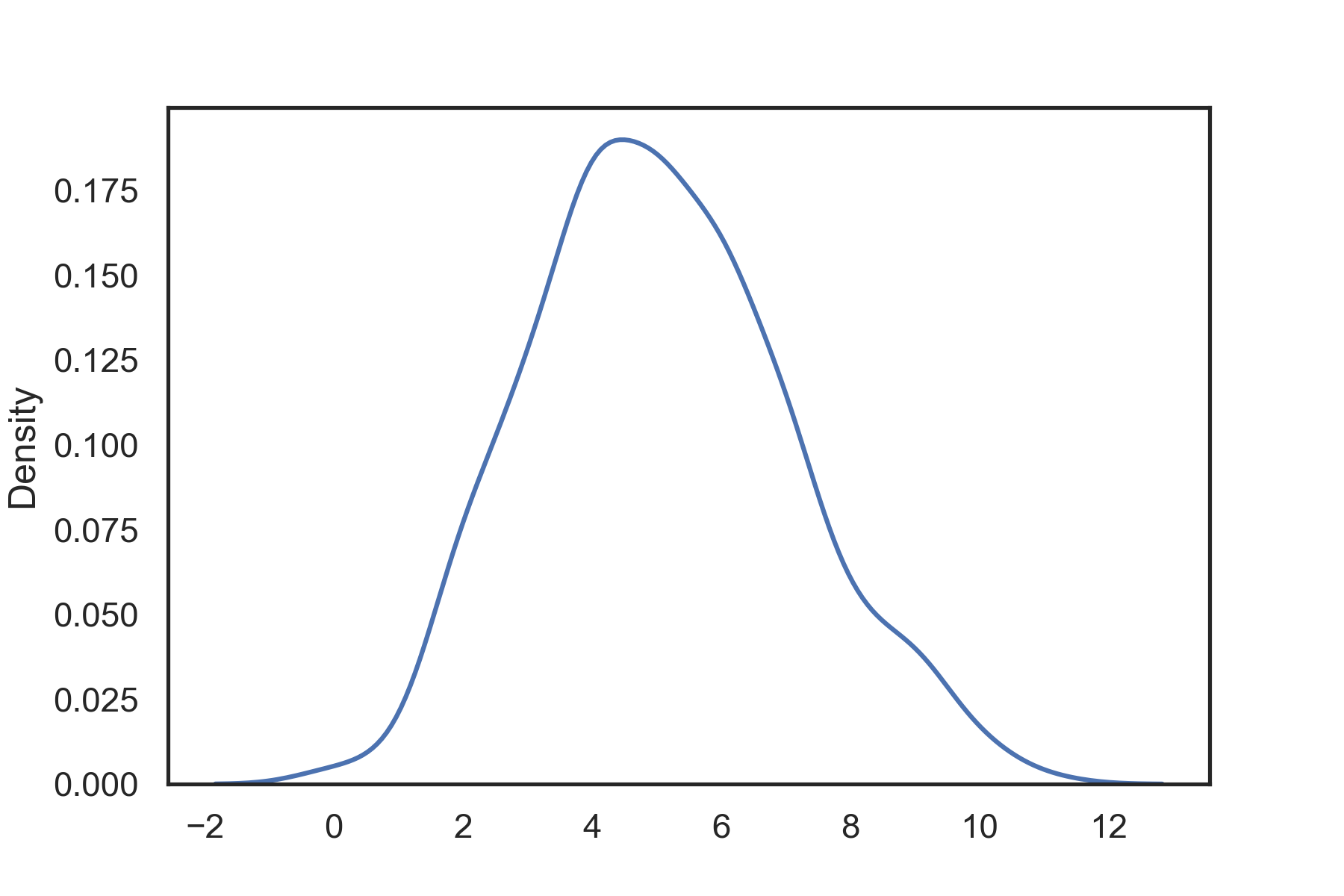
But now, let’s imagine this is one of many villages, each with its own propensity to find these treasures magically. Le’s measure these villages’ treasure-finding probability per day over a year.
Binomial distribution of 10 villages each with 20 huts. the likelihood of finding a treasure (p) for a hut is 0.25. Max likelihood is 5 treasures per day when measured over a year.
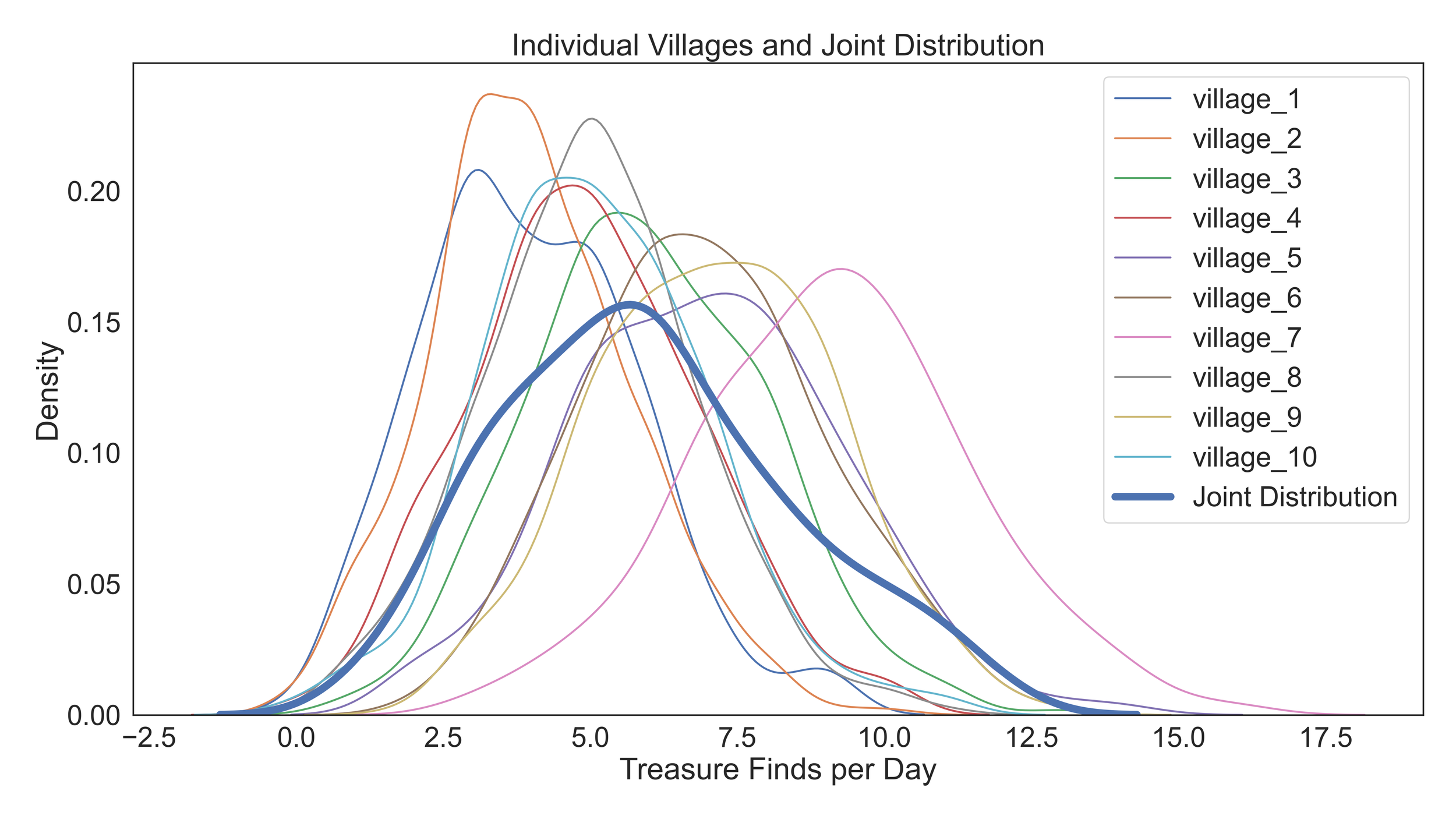
In the beginning, our 10 villages were identical in their probability of finding treasure per day, and in the MI talk, we can’t know where a villager lives if he told us how many treasures he found last year as the joint distribution (the average distribution of all villages seems very similar to each village).
But as villages change and the spirits play their game, each village develops its own unique identity. As they do, the joint distribution describes them less and less.
The distance between the joint distribution and the average distribution in terms of entropy is the formal meaning of MI. In this case, MI = 0.281. This means that if a villager were to tell you how many treasures, on average, their village finds in a day, it would lower your uncertainty by 0.281. To get an intuition about what this means, let’s dive into what it means to “know” something.
Well, we have 10 villages. To guess the home village of a random villager, we would need to eliminate 9 erroneous villages. As each bit of information lowers our uncertainty by half, the first bit leaves us with 5 villages, the second bit lowers it to 2.5 villages, and so on, so to be completely certain, we would need roughly 4 bits.
This could be easily calculated from the following:
bits = ⌈log2N⌉
So for N = 10
bits = ⌈log210⌉ = ⌈3.3219⌉ = 4
This would have to mean that there is no overlap between villages at all:
When we calculate MI for this village map, we get MI = 3.273, which means we have eliminated all uncertainty about the village just by the villager telling us the average number of treasures found last year! If you look at the graph, it is pretty apparent. As there is almost no overlap between villages, there is no probability of being wrong.
Mutual Information, in essence, tells us how much we can know about one thing from observing another. How ripe is a banana just by its color? How cold is the water in the ocean just from the color of the sky? Many living things, including us, rely on such associations. Strong prior knowledge, coupled with simple, robust rules, can transcend space and enable communal decisions that span great distances. This is how a young queen bee knows her would-be grooms are expecting her in her nuptial flight and how corals can release their gametes into the vast ocean, hoping that somehow, somewhere, they will meet their counterparts. These simple yet powerful rules that relay knowledge might very well be the foundation of life itself